Overview
Quantum field theory (QFT) is the framework within which fundamental physics is formulated. It provides an extremely powerful set of methods to compute observables emerging from the interactions of elementary particles at highest energies. It has led to the most spectacular agreement between theoretical predictions and observations performed with the most sophisticated experiments that mankind has ever conducted. It provides deep insights into the nature of our universe and allows us to study alternative possible and self-consistent universes. At the same time its foundations remain a subject of present day research. It isgenerally believed that Poincaré symmetry (plus possible extensions such as conformal and/or supersymmetry), locality and internal gauge symmetries constitute fundamental structures. The traditional approach to QFT starts out from a classical action formulation, reflecting the underlying symmetries and chosen field contents in the given space-time dimension. This classical theory is then quantized, most efficiently by using Feynman’s path integral formalism. In a perturbative setting this provides the traditional route for arriving at the Feynman diagrammatic expansion, allowing for the perturbative computation of a multitude of possible observables – at least in principle. Employing a lattice discretization of space-time yields a non-perturbative definition of the path integral, allowing us to study observables not accessible by perturbative QFT. Clearly, symmetries play a constitutional rôle in the formulation of QFTs. Studies on dualities between QFTs of various dimensions reveal a rich interconnected landscape of QFTs, notably also including gravitational interactions.
The research activities of the RTG focus on the following challenges for current research in QFT that tie together various individual subprojects:
- Establishing novel tools for high precision QFT predictions combined with agnostic approaches in the search for new physics beyond the standard model.
- Accessing the strong coupling regime in QFTs by employing innovative methods and dualities.
- Unraveling hidden algebraic structures and dualities in QFTs, thereby clarifying their rôle in the quest for quantum gravity.
The research agenda of this RTG is to work on on these challenges by questioning and improving the foundations and traditional methods in QFT as well as quickly transferring advances made in one sector of our fields to another. In short, together with our early stage researchers we will rethink quantum field theory.
The research program of our RTG is structured in the six main subareas:
- Scattering amplitudes
- Phenomenology
- Lattice field theory
- AdS/CFT correspondence
- Gravitational waves
- Mathematical aspects of QFT
They reflect the expertise of the researchers involved and lead to challenging and timely projects at the doctoral and postdoctoral level. A recurrent theme of our research will be the cross-fertilization of these sub areas by transferring innovations from one area to another based on common interests of the groups involved, thereby providing an added value of the RTG.
The interconnections of our subfields are sketched graphically as
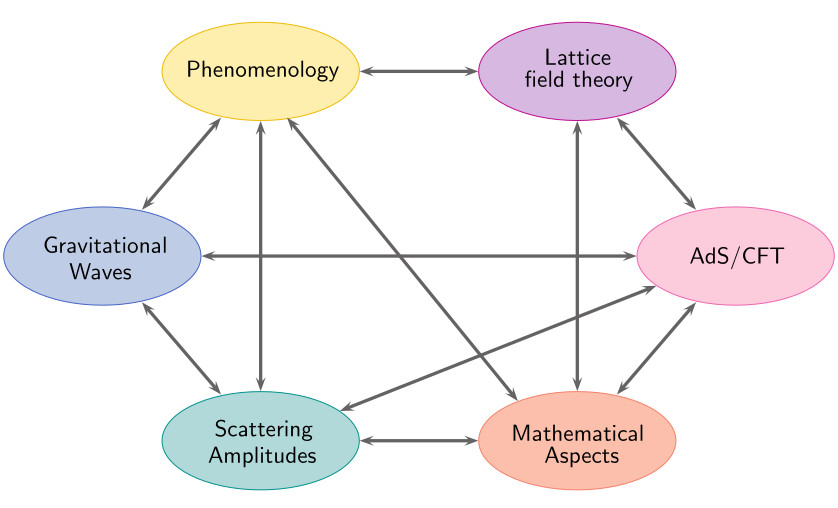
and are detailed on separate pages.

