Principal investigators: Gaetan Borot, Olaf Hohm
Doctoral researchers: Tomas Codina, Allison Pinto, Davide Scazzuso
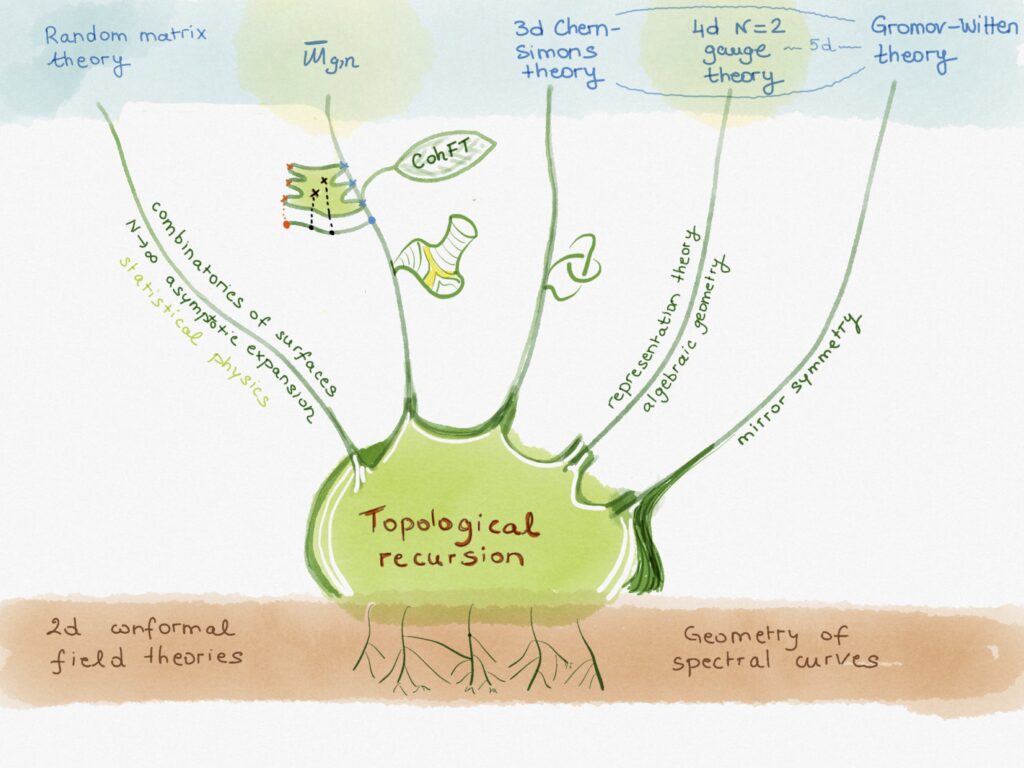
Topological recursion, enumerative geometry and QFT
In this research area we focus on the interrelations between various aspects of algebra, geometry and quantum field theory investigated from the unifying perspective of topological recursion, which can be thought as a recursion on the topology of the worldsheet.
Main topics
- Intersection theory on the moduli space of curves
- Topological string theory and mirror symmetry
- Topological quantum field theories
- 2d conformal field theory and W-algebras
- N = 2 supersymmetric gauge theories of class S
- Geometry of spectral curves
- Integrable systems
- 2d statistical physics on random surfaces
- Random matrix models, combinatorics and geometry of random surfaces
L∞-algebras in Quantum Field Theory
This aspect of the research program is concerned with higher algebraic structures in QFT and, more generally, in theoretical and mathematical physics.
Lie groups and Lie algebras are the structures underlying most of contemporary fundamental physics, from the standard model of particle physics to Einstein’s theory of general relativity. Recent developments have shown that higher algebraic structures in form of
L∞-algebras could play an important role for the physics of the 21st century.
- L∞-algebras are a generalisation of Lie algebras satisfying higher Jacobi identities involving potentially infinitely many higher brackets. It has become clear recently that L∞-algebras can function naturally as the organisational principle for arbitrary field theories
- A powerful machinery for L∞-algebras exists —homotopy transfer—that has recently been argued to govern dualities of QFT
- There are rich sub-theories of full string theory that include massive string modes in a duality covariant formulation that are not captured by the usual spacetime theories such as supergravity. The explicit construction of such theories and the determination of their underlying L∞-algebras is the focus of current research
- Higher-derivative α’-corrections in string inspired gravitational theories could play a role in resolving the big-bang singularity or in providing a non-perturbative mechanism to generate de Sitter vacua.
L∞-algebras within the framework of double field theory can help in understanding the symmetry principles of these corrections
Integration into the RTG
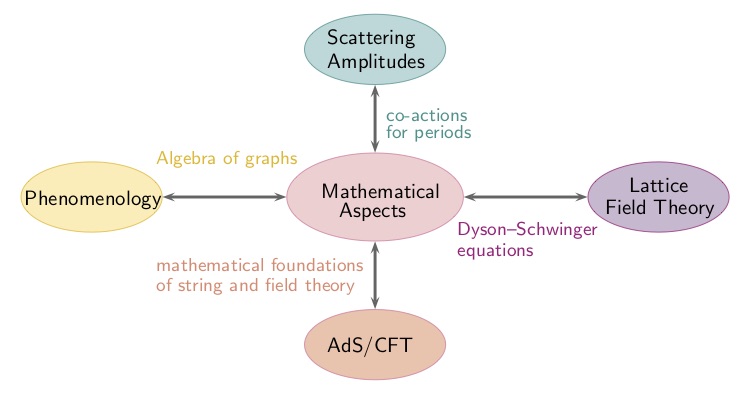
This research topic integrates well into the RTG as it provides mathematical foundations for phenomenology, scattering amplitudes, the AdS/CFT correspondence and for perturbative expansions in terms of Feynman diagrams.
The spacetime formulation provided by double field theory is a promising framework in order to understand the principles underlying the “double copy” construction for the computation of amplitudes.