 Principal investigators: Jan Plefka, Peter Uwer, Olaf Hohm
Principal investigators: Jan Plefka, Peter Uwer, Olaf Hohm
Postdoctoral researcher: Gustav Uhre Jakobsen, Kays Haddad, Gustav Mogull
Doctoral reseachers: Mathias Driesse, Marie Ernø-Møller, Jitze Hoogeveen, Benjamin Sauer
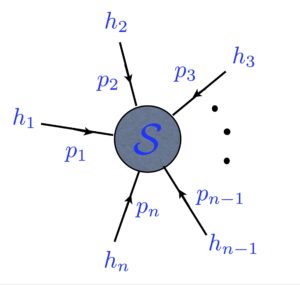
Scattering amplitudes are a central prediction of quantum field theories, providing the link to collider experiments and cosmological or astrophysical observations. However, the celebrated Feynman diagram expansion for computing these core quantities — originating from a Lagrangian description of QFT — becomes prohibitively challenging when considering processes with many scattered particles or at high-loop orders (high-order quantum corrections). This situation is particularly dramatic in Yang-Mills theory and even more so in perturbative quantum gravity due to their involved vertex structures. Yet the final expressions are often surprisingly simple when expressed in suitable variables which make the physical properties (on-shell relations for momenta and polarizations) manifest. This situation hints at an alternative formulation of QFT that solely uses on-shell data. This vision has grown into a dedicated research program in recent years, bringing together researchers from phenomenological, formal theoretical and even mathematical backgrounds. Recursive techniques fusing lower-point amplitudes into higher-point ones have yielded complete analytic solutions for tree-level processes at any multiplicity in theories with and even without supersymmetry. Here the Britto-Cachazo-Feng-Witten (BCFW) on-shell recursion relation and its supersymmetric generalizations have proven most efficient and should now be included in general QFT textbooks. Beyond this, a set of complementary on-shell techniques for expressing gluon and graviton tree-level amplitudes has been developed in the past few years that manifests particular properties of scattering amplitudes: The Graßmannian and amplituhedron formulation of supergluon amplitudes has been most influential in connecting to mathematics and integrability aspects and is tightly bound to the momentum twistor variables resolving all on-shell conditions. The Cachazo-He-Yuan (CHY) formalism employing the scattering equations provides a unifying representation connecting gravity, gluon and bi-adjoint scalar amplitudes (and more). It has proven highly effective for proving subleading soft theorems and for uncovering surprising relations between gravity-matter and gluon-matter tree-level amplitudes. Moreover, loop amplitudes are strongly constrained by unitarity cuts — a consequence of probability conservation in quantum mechanics. Artfully exploiting these constraints enables one to reduce loop-level computations to tree-level data, a technique known as generalized unitarity. This novel technique has boosted computational progress in phenomenology, where the computation of one-loop processes is now entirely automatized.
Beyond this, a set of complementary on-shell techniques for expressing gluon and graviton tree-level amplitudes has been developed in the past few years that manifests particular properties of scattering amplitudes: The Graßmannian and amplituhedron formulation of supergluon amplitudes has been most influential in connecting to mathematics and integrability aspects and is tightly bound to the momentum twistor variables resolving all on-shell conditions. The Cachazo-He-Yuan (CHY) formalism employing the scattering equations provides a unifying representation connecting gravity, gluon and bi-adjoint scalar amplitudes (and more). It has proven highly effective for proving subleading soft theorems and for uncovering surprising relations between gravity-matter and gluon-matter tree-level amplitudes. Moreover, loop amplitudes are strongly constrained by unitarity cuts — a consequence of probability conservation in quantum mechanics. Artfully exploiting these constraints enables one to reduce loop-level computations to tree-level data, a technique known as generalized unitarity. This novel technique has boosted computational progress in phenomenology, where the computation of one-loop processes is now entirely automatized. 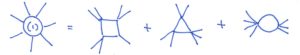 Importantly, the building blocks of the one-loop unitarity construction are the tree-level diagrams constructed by the tools discussed above. In fact, results based on purely theoretical considerations, such as the complete tree-level S-matrix of N=4 super Yang-Mills theory, have found phenomenological applications by implementing the resulting analytical formulas for mass less QCD amplitudes in the numerical codes.
Importantly, the building blocks of the one-loop unitarity construction are the tree-level diagrams constructed by the tools discussed above. In fact, results based on purely theoretical considerations, such as the complete tree-level S-matrix of N=4 super Yang-Mills theory, have found phenomenological applications by implementing the resulting analytical formulas for mass less QCD amplitudes in the numerical codes.
Importantly, these developments are far more than a mere technical innovation. They shed light on powerful new mathematical structures present at the heart of QFT. They suggest that trusted entities of QFT such as unitarity, locality and even space-time itself become emergent concepts. A fascinating and still poorly understood hidden symmetry structure that has emerged from these studies is the color-kinematical duality. It represents gravity by two copies of Yang-Mills theories. This so-called double-copy construction, due to Bern, Carrasco and Johansson (BCJ), assembles multi-loop amplitudes in gravity from squares of suitably arranged building blocks of their Yang-Mills counterparts.The particular representation of gauge-theory amplitudes suitable for the double-copy construction is based on the idea of treating the color and kinematic degrees of freedom on equal footing: The color degrees of freedom in a non-Abelian gauge theory enter through contracted structure constants of the gauge group which are naturally associated with cubic graphs, and constructed from trivalent vertices. Also the kinematic degrees of freedom in gauge-theory amplitudes — momenta and polarizations — can always be grouped into a cubic graph language. According to the BCJ duality or color-kinematic duality, the kinematic representatives of cubic graphs can be arranged to satisfy the same Jacobi identities as the structure constants from the color representative.
Integration into the RTG
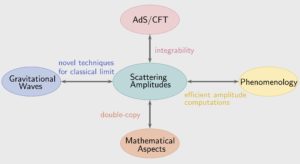
This is a particularly integrative area for the RTG as ultimate applications lie in phenomenology and it connects to fundamental questions of symmetries and dualities.


 Principal investigators: Jan Plefka, Peter Uwer, Olaf Hohm
Principal investigators: Jan Plefka, Peter Uwer, Olaf Hohm