Principal investigators: Agostino Patella, Rainer Sommer
Postdoctoral researcher: Johannes Weber
Doctoral researchers: Alexander Broll, Jens Lücke
Low-energy properties of QCD are dominated by non-perturbative physics. For instance, hadron spectra and interactions are not correctly described at any order in the perturbative expansion. Although a variety of analytical techniques have been developed to capture certain non-perturbative effects in highly symmetric quantum field theories, these techniques are typically not available for QCD.
Lattice QCD is the only known consistent way to define QCD non-perturbatively. In a compact spacetime, the lattice-discretized QCD functional integral becomes a regular integral on a compact manifold, even without gauge fixing. Besides being mathematically well defined it can be evaluated numerically by means of Monte Carlo techniques. Continuous QFT is recovered by sending the lattice spacing (i.e. the inverse UV cutoff) to zero and the box size to infinity. In practice these limits are taken by numerical extrapolation, guided by scaling laws determined by means of effective field theory techniques.
Lattice QCD calculations have seen tremendous progress in recent years, thanks to theoretical and algorithmic advancements, in conjunction with the constant growth of computer power per Euro. Observables once thought to be out of reach for lattice calculation are now being explored. For instance, calculations of scattering amplitudes for light hadrons. Strategies to determine parton distribution functions are being investigated. Classical observables have been pushed to an unprecedented degree of precision, typically at the one-percent level. Prominent examples are the strong coupling constant, the pion and kaon decay constants, and semileptonic form factors.
The research program of the RTG 2575 is built around the following four pillars:
Heavy-quark physics
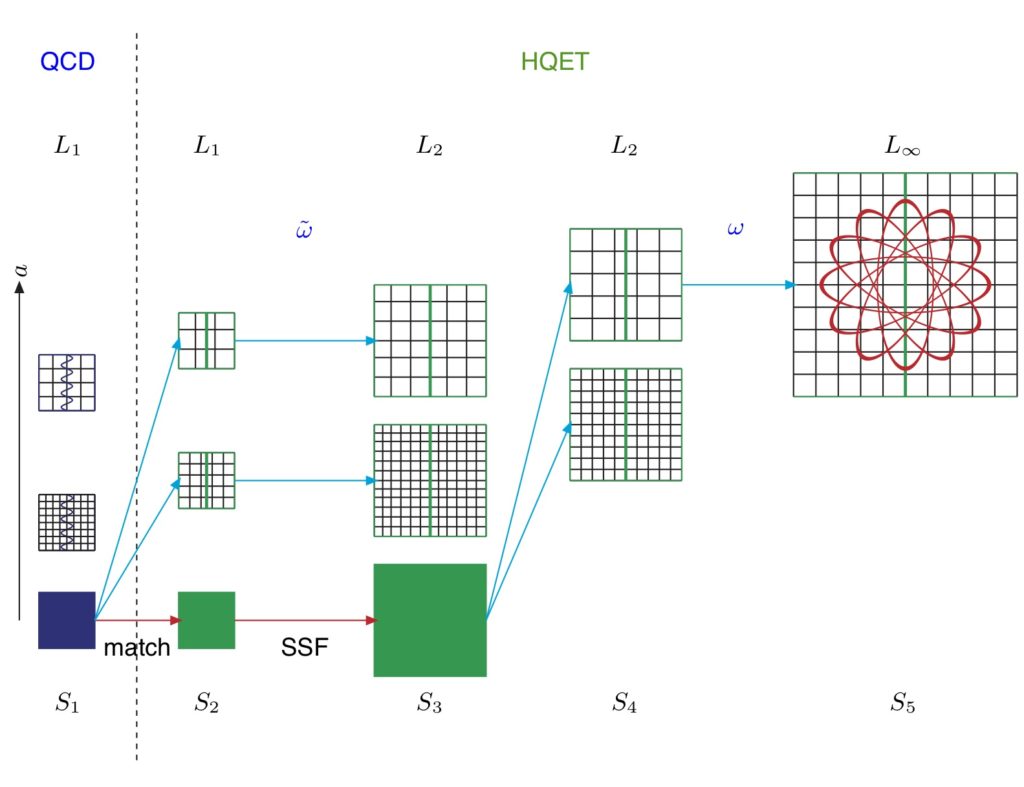
The decays, in particular semi-leptonic, of B-mesons play a crucial role in flavor physics, and in indirect searches for new Physics. Understanding the QCD matrix elements quantitatively is essential in order to correctly interpret observed decay, especially from Belle-II. Accommodating light up, down and strange quarks and a heavy bottom quark simultaneously in a lattice simulation is computationally prohibitive at present. The best available approach is to use an effective-theory description of the bottom quark, the Heavy-quark effective theory (HQET). It provides the correct framework to calculate heavy-light meson physics in a systematic expansion in inverse powers of the bottom quark mass.
More information:
- Non-perturbative Heavy Quark Effective Theory: Introduction and Statuts
Rainer Sommer, Nucl. Part. Phys. Proc., Vol. 261-262, 338 (2015)
article on ScienceDirect e-print on arXiv - Continuum limit of the leading-order HQET form factor in Bs to K e nu decays
Felix Bahr et. al., Phys. Lett. B 757, 473 (2016)
article on ScienceDirect e-print on arXiv
Isospin-breaking and radiative corrections
Most lattice QCD simulations available up to date are performed in the isospin-symmetric limit, i.e. assuming degenerate up and down quark masses. In addition, the coupling to the electromagnetic field is typically ignored. However, at the percent level precision isospin-breaking corrections and particular QED radiative corrections must be included, for instance in the determination of the pion and kaon decay constants. Recently a lot of activity has been devoted to develop a consistent and usable definition of QED and charged states in finite volume. The use of C-periodic boundary conditions is a theoretically-sound setup to describe charged states in a periodic box.
The RTG works on two main challenges: On the algorithmic side, improved algorithms for non-degenerate up- and down quarks are developed. On the conceptual side, a theoretically sound setup to calculate decay rates integrated over the soft-photon energies (a la Bloch and Nordsieck) from finite volume Euclidean QED is formulated.
Advancements in methodology
One of the challenges in lattice calculations lies in finding efficient and sound strategies to renormalize composite operators. These arise naturally as effective vertices at low energy, generated by the electroweak interactions and by extensions of the SM. A new handle on renormalization on the lattice is the gradient flow, a recently-proposed QFT concept. The original QFT is coupled to a fictitious fifth dimension in which all fields propagate. The dynamics in the fifth dimension is classical and does not back-react onto the original four-dimensional theory. Composite operators away from the 4-dimensional boundary have a dramatically simplified renormalization pattern, and often do not renormalize at all. In principle the gradient flow can be used an as intermediate renormalization scheme; still, much work is needed to turn this idea into a robust and viable computational tool.
Non-QCD theories
Besides QCD, the lattice discretization and numerical simulations can be used to investigate the non-perturbative regime of other quantum field theories. Typical examples are gauge theories in the conformal window, supersymmetric gauge theories, technicolor models, models for partially-composite Higgs, and strongly-coupled dark matter. This avenue is interesting for its phenomenological implications, but also from a purely conceptual point of view.

