Principal investigators: Valentina Forini, Matthias Staudacher, Agostino Patella, Jan Plefka, Stijn van Tongeren
Postdoctoral researchers: Rob Klabbers
Doctoral researchers: Ilaria Costa, Moritz Kade, Roman Stemplowski
The Anti-de Sitter/conformal field theory correspondence (AdS/CFT) is the first and most precisely defined example of a gauge/gravity duality. It holographically relates a quantum field theory in flat four-dimensional space-time to a string theory moving in a curved five-dimensional space-time. This constitutes a revolutionary way of thinking about quantum field theory. While a mathematical proof is still absent, manifold approaches continue to be developed that powerfully test this conjecture. All of these have, up to now, led to spectacular confirmation.
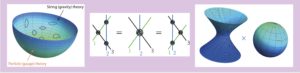
One class of conjecture-verifying methods rests on the discovery that planar/free AdS/CFT is integrable, leading to a multitude of exactly computable quantities that agree with both QFT and string theory. Typically, the derivations involve a combination of string theoretic and field theoretic techniques, where one e.g. combines insights from sophisticated string theory sigma models with spin chain structures emerging from the gauge theories in their perturbative regime
.
This is a prime example for the rethinking of QFT as envisioned by the RTG. So far the majority of results have been for the simplest interacting gauge theory in four dimensions: Planar N=4 Super Yang-Mills Theory (SYM). Still, it is generally believed that the lessons learned from the exact solution of this model will lead to novel ways of performing calculations in more realistic theories. In fact, the study of various deformations of this simplest set-up have recently come into focus.
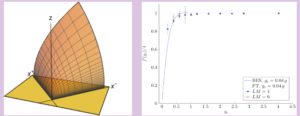
Another even more recent „ab initio‘‘ approach employs lattice field theory for the worldsheettheory of the AdS superstring. It neither assumes AdS/CFT nor integrability. Its two-dimensional setup it is a powerful way for verifying at arbitrary coupling and in full generality the holographic conjecture in those cases where exact methods presumably do not exist (non-integrable backgrounds) or are not yet available (e.g. correlators of string vertex operators dual to gauge theory correlators).
Integration into the RTG
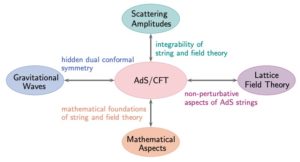
AdS/CFT is connected to most other research directions of the RTG: 1. it inspires novel techniques for scattering amplitudes; 2. it suggests non-perturbative studies of worldsheet AdS strings with lattice field theory methods; 3. it unearthes deep mathematical structures such as Yangian and Hopf algebras, with potential clues on the mathematical foundations of QFT; 4. it relates to gravitational wave research (e.g. the ”effective one-body formalism for gravitational waves was recently connected to AdS/CFT integrability via a hidden dual conformal symmetry). Future links to phenomenology might eventually emerge as well.

