Trainingsprogramm zu formalen Techniken linguistischer Analyse
Zwei Formeln sind äquivalent genau dann, wenn sie unter denselben Bedingungen wahr sind / dieselben Wahrheitsbedingungen haben.
Test: Tabelle mit Wahrheitsverteilung für die Formeln
Verfahren:
Herleitung der Wahrheitswertverteilung für die Gesamtformel über die Wahrheitswertverteilung der Teilformeln
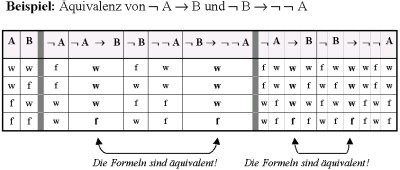
Zeigen Sie anhand von Wahrheitswerttabellen, ob die Formeln äquivalent sind!
1. A -> B (Bsp.: "Wenn Uta anruft, freut sich Kai.") 2.  A \/ B(Bsp.: "Uta ruft nicht an, oder Kai freut sich.") |  | |
1. A <-> B(Bsp.: "Genau dann, wenn Uta nicht anruft, freut sich Kai.") 2. B <-> A(Bsp.: "Genau dann, wenn Kai sich nicht freut, ruft Uta an") | | |
1. A -> B(Bsp.: "Wenn Uta anruft, freut sich Kai nicht.") 2. A -> B(Bsp.: "Wenn Uta nicht anruft, freut sich Kai.") | |
| Suche |
| Kontakt | Impressum |